how to draw 3d coordinate system
Some basic 3D axes with spherical and cylindrical coordinates, unit vectors, area chemical element and solid angle.
For more figures of coordinate organisation, have a look at the "coordinates" tag.
Spherical coordinates:
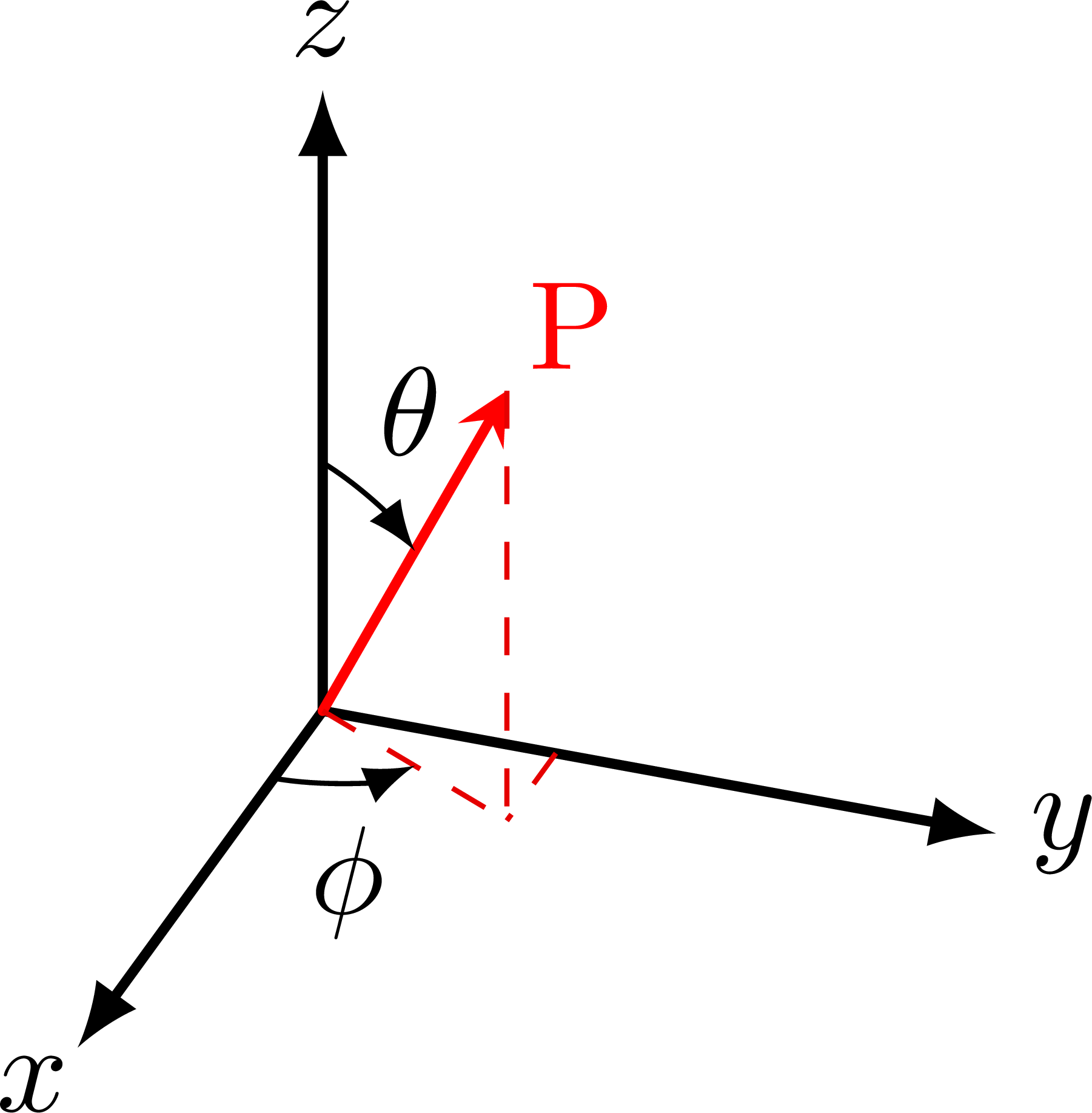
Spherical coordinates with x, y, z unit vectors:
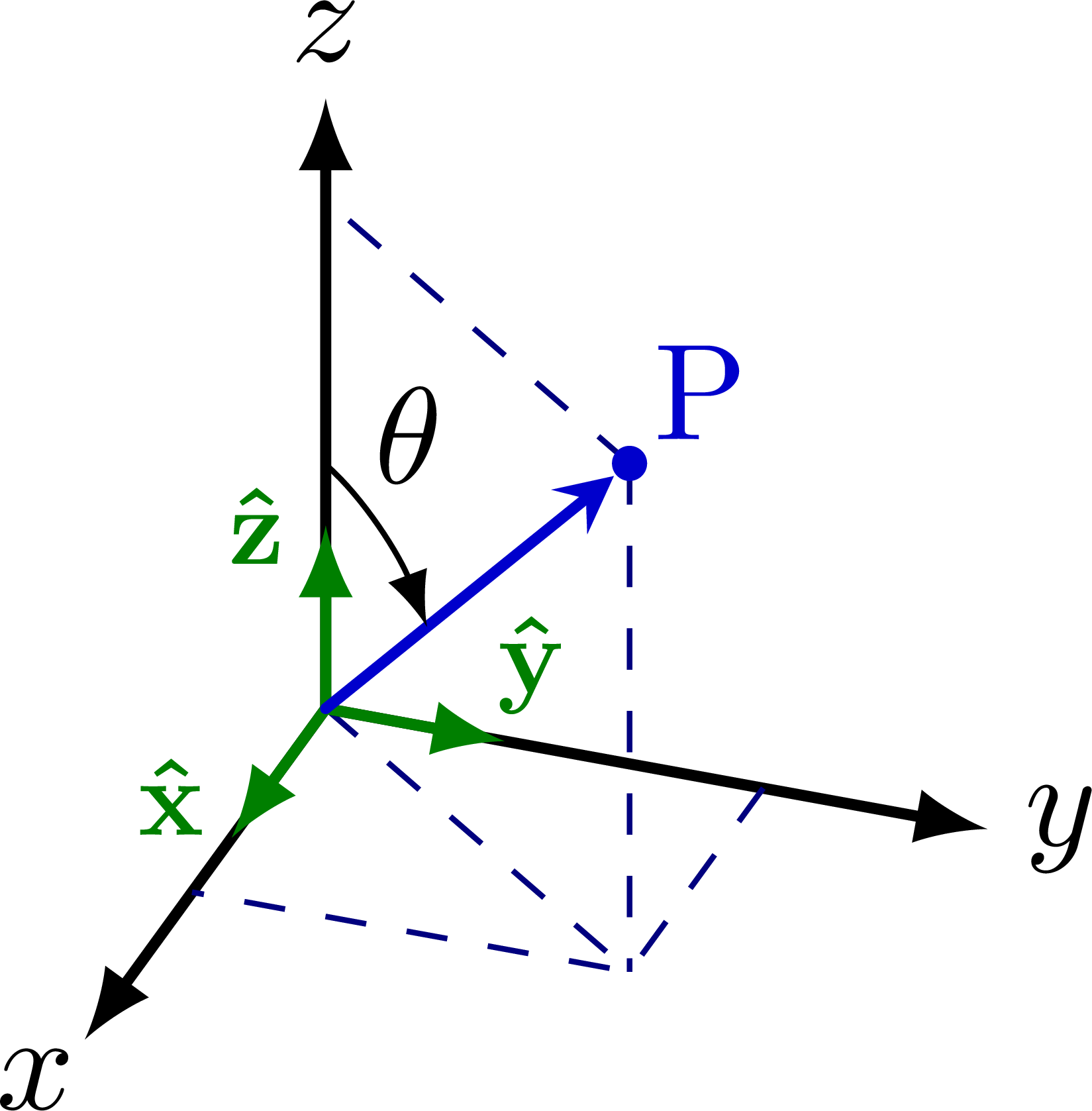
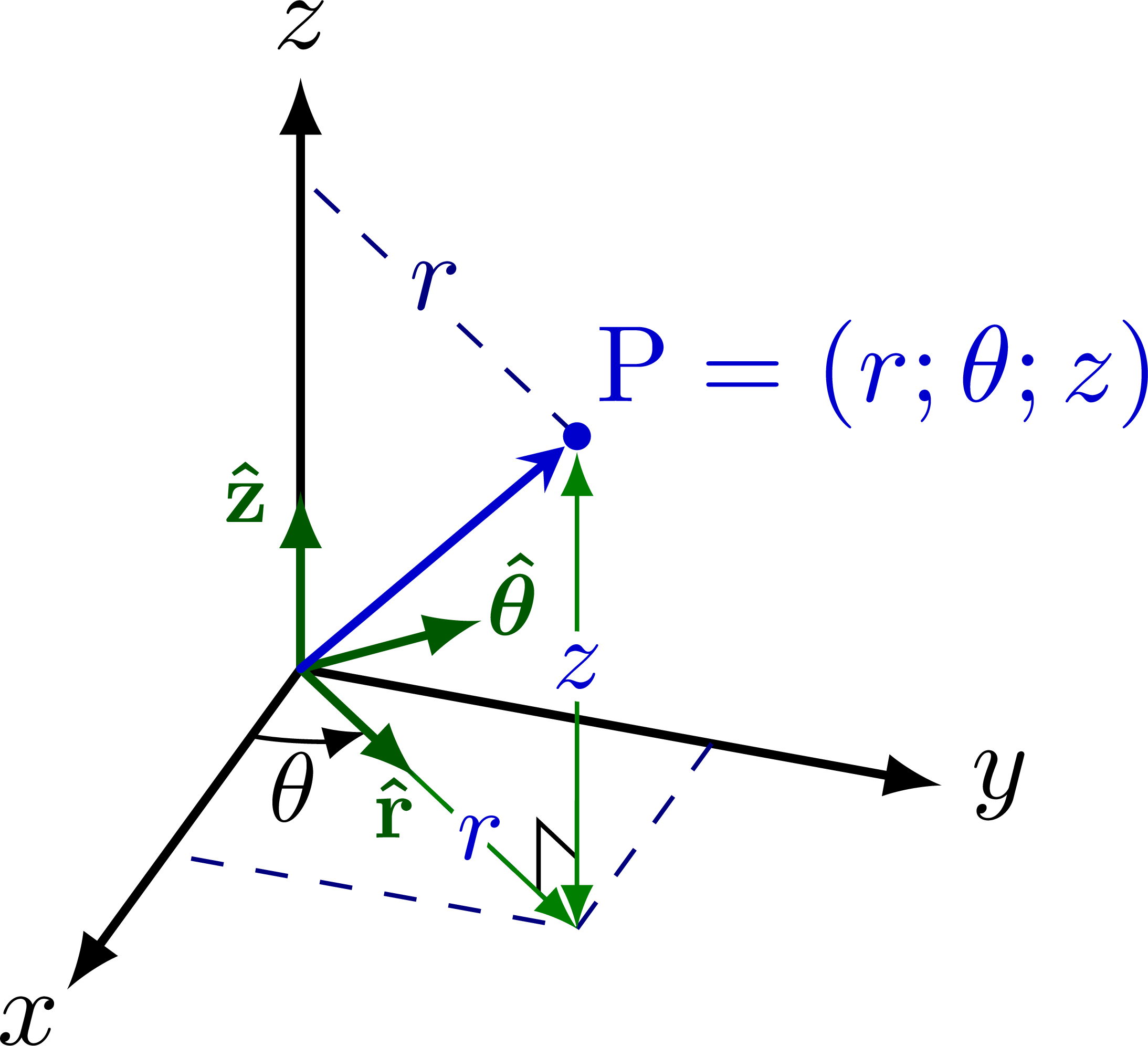
Cylindrical coordinates:
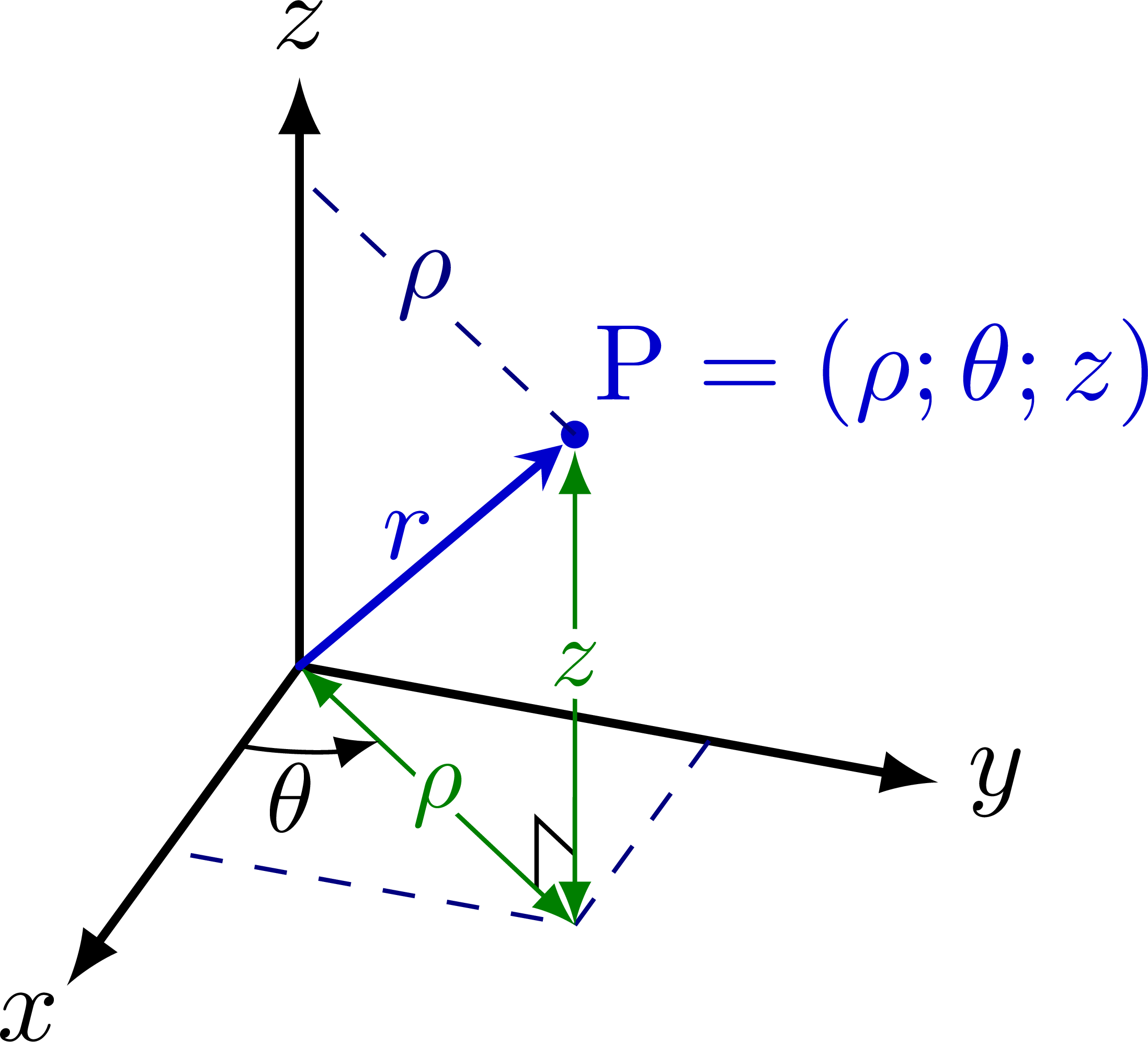
Cylindrical coordinates with unit vectors:
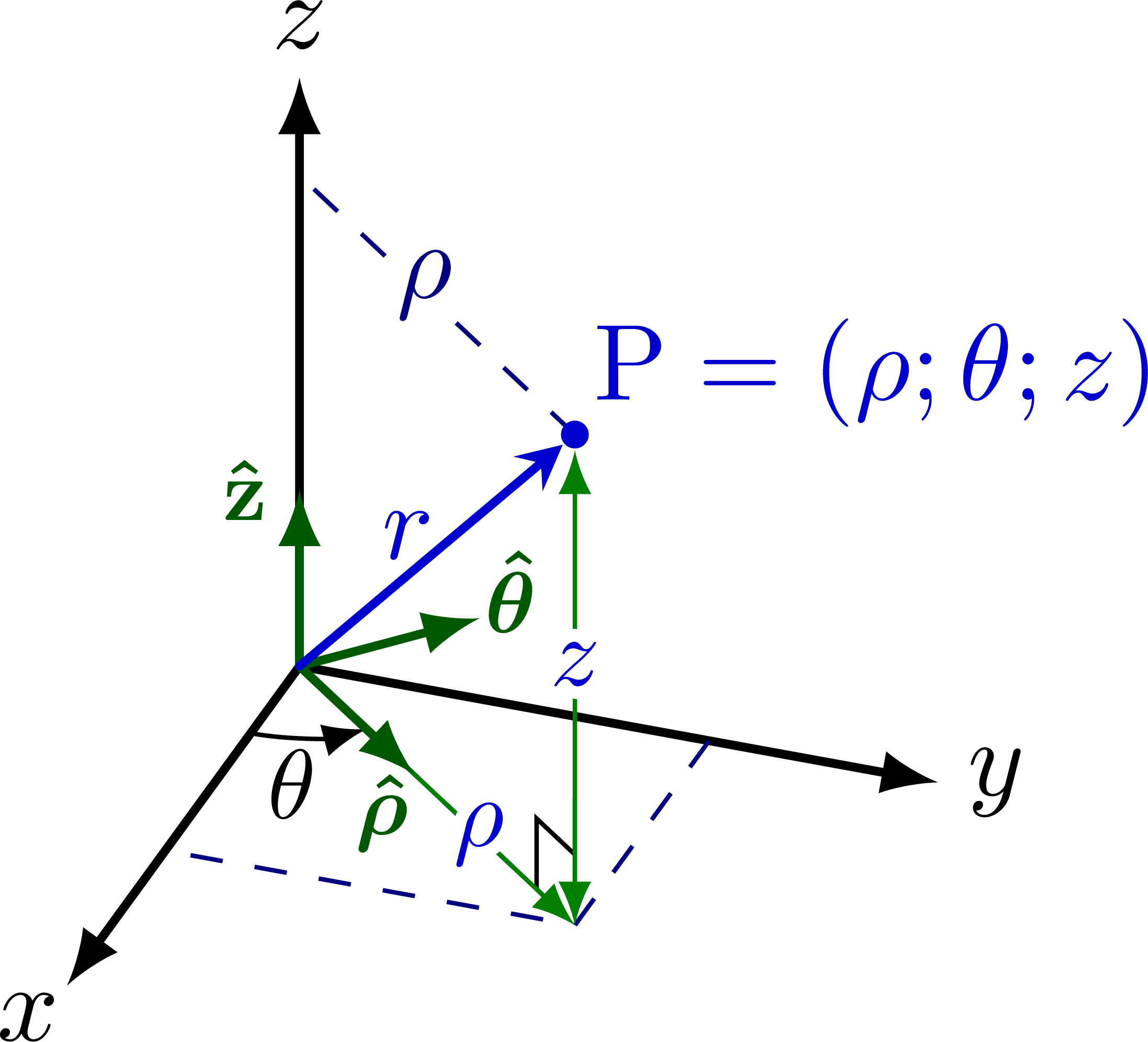
Cylindrical coordinates with rho and r swapped:
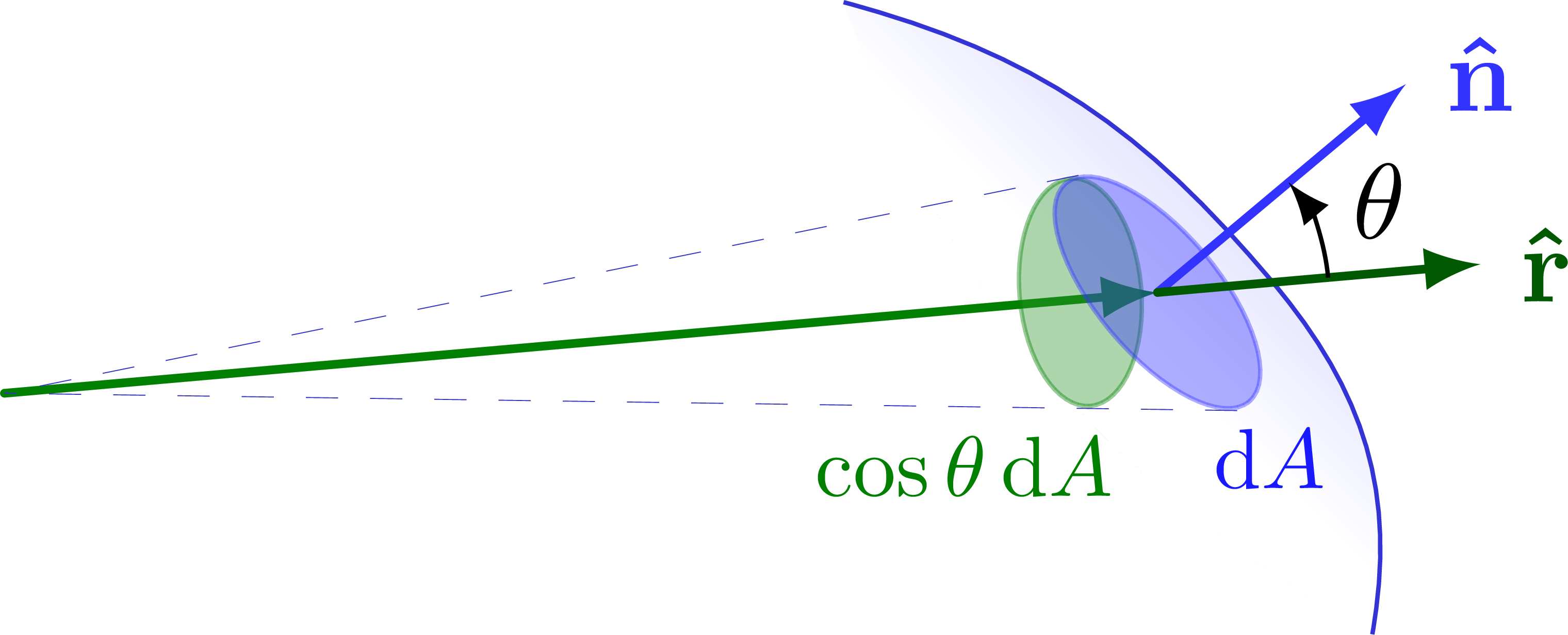
Surface integral over spherical coordinates:

Integrating over a surface:
Edit and compile if you similar:
% Author: Izaak Neutelings (June 2017) % taken from https://tex.stackexchange.com/questions/159445/draw-in-cylindrical-and-spherical-coordinates \documentclass[border=3pt,tikz]{standalone} \usepackage{physics} \usepackage{tikz} \usepackage{tikz-3dplot} \usepackage[outline]{profile} % glow effectually text \usepackage{xcolor} \colorlet{veccol}{dark-green!50!blackness} \colorlet{projcol}{blueish!70!black} \colorlet{myblue}{bluish!lxxx!blackness} \colorlet{myred}{red!90!black} \colorlet{mydarkblue}{blue!50!black} \tikzset{>=latex} % for LaTeX arrow caput \tikzstyle{proj}=[projcol!80,line width=0.08] %very sparse \tikzstyle{area}=[draw=veccol,make full=veccol!80,fill opacity=0.6] \tikzstyle{vector}=[-stealth,myblue,thick,line cap=round] \tikzstyle{unit of measurement vector}=[->,veccol,thick,line cap=round] \tikzstyle{nighttime unit vector}=[unit of measurement vector,veccol!seventy!black] \usetikzlibrary{angles,quotes} % for pic (angle labels) \contourlength{1.3pt} \begin{certificate} % 3D Centrality with spherical coordinates \tdplotsetmaincoords{60}{110} \begin{tikzpicture}[scale=2,tdplot_main_coords] % VARIABLES \def\rvec{.eight} \def\thetavec{30} \def\phivec{60} % AXES \coordinate (O) at (0,0,0); \draw[thick,->] (0,0,0) -- (1,0,0) node[below left=-3]{$x$}; \draw[thick,->] (0,0,0) -- (0,ane,0) node[correct=-1]{$y$}; \draw[thick,->] (0,0,0) -- (0,0,1) node[in a higher place=-i]{$z$}; % VECTORS \tdplotsetcoord{P}{\rvec}{\thetavec}{\phivec} \draw[vector,red] (O) -- (P) node[above right=-2] {P}; \describe[dashed,myred] (O) -- (Pxy); \draw[dashed,myred] (P) -- (Pxy); \draw[dashed,myred] (Py) -- (Pxy); % ARCS \tdplotdrawarc[->]{(O)}{0.ii}{0}{\phivec} {anchor=north}{$\phi$} \tdplotsetthetaplanecoords{\phivec} \tdplotdrawarc[->,tdplot_rotated_coords]{(0,0,0)}{0.4}{0}{\thetavec} {anchor=south west}{\hspace{-1mm}$\theta$} \finish{tikzpicture} % 3D AXIS with spherical coordinates \tdplotsetmaincoords{sixty}{110} \begin{tikzpicture}[scale=1.viii,tdplot_main_coords] % VARIABLES \def\50{0.3} % length scale night unit vector \def\rvec{ane.two} \def\thetavec{46} \def\phivec{l} % AXES \coordinate (O) at (0,0,0); \tdplotsetcoord{P}{\rvec}{\thetavec}{\phivec} \draw[dashed,mydarkblue] (O) -- (Pxy); \describe[thick,->] (0,0,0) -- (1,0,0) node[below left=-three]{$ten$}; \draw[thick,->] (0,0,0) -- (0,1,0) node[right=-one]{$y$}; \draw[thick,->] (0,0,0) -- (0,0,1) node[above=-one]{$z$}; \draw[unit vector] (0,0,0) -- (1.3*\fifty,0,0) node[above=3,left=-1,scale=0.viii]{$\vu{x}$}; \draw[unit of measurement vector] (0,0,0) -- (0,.ix*\fifty,0) node[right=2,in a higher place=-1,scale=0.8]{$\vu{y}$}; \draw[unit vector] (0,0,0) -- (0,0,\50) node[left,scale=0.8]{$\vu{z}$}; % VECTORS \describe[dashed,mydarkblue] (P) -- (Pxy); \depict[dashed,mydarkblue] (P) -- (Pz); \draw[dashed,mydarkblue] (Py) -- (Pxy) -- (Px); \node[circle,inner sep=0.9,make full=myblue] (P') at ({\rvec*sin(\thetavec)*cos(\phivec)},{\rvec*sin(\thetavec)*sin(\phivec)},{\rvec*cos(\thetavec)}) {}; \depict[vector] (O) -- (P') node[above right=-2] {P}; % ARCS \tdplotsetthetaplanecoords{\phivec} \tdplotdrawarc[->,tdplot_rotated_coords]{(0,0,0)}{0.4}{0}{\thetavec} {right=2,above}{$\theta$} \end{tikzpicture} % 3D AXIS with cylindrical coordinates \tdplotsetmaincoords{60}{110} \begin{tikzpicture}[scale=2.2,tdplot_main_coords] % VARIABLES \def\rtheta{0.25} % length theta arc \def\rvec{i.2} \def\phivec{46} \def\thetavec{48} % AXES \coordinate (O) at (0,0,0); \draw[thick,->] (0,0,0) -- (1,0,0) node[below left=-3]{$x$}; \draw[thick,->] (0,0,0) -- (0,1,0) node[right=-1]{$y$}; \describe[thick,->] (0,0,0) -- (0,0,1) node[above=-1]{$z$}; % Betoken P \tdplotsetcoord{P}{\rvec}{\phivec}{\thetavec} \draw (Pxy)++(0,0,0.12) --++ (\thetavec+180:0.12) --++ (0,0,-0.12); \node[circumvolve,inner sep=0.nine,fill=myblue] (P') at ({\rvec*sin(\phivec)*cos(\thetavec)},{\rvec*sin(\phivec)*sin(\thetavec)},{\rvec*cos(\phivec)}) {}; % VECTORS & DASHED \draw[dashed,mydarkblue] (P) -- (Pz) node[pos=0.55,to a higher place right=-six] {\profile{white}{$\rho$}}; \describe[dashed,mydarkblue] (Py) -- (Pxy) -- (Px); % MEASURES \describe[<->,veccol] (0,0,0) -- (\thetavec:{\rvec*sin(\phivec)}) node[pos=0.5,scale=0.9]{\contour{white}{$\rho$}}; \draw[<->,veccol] (\thetavec:{\rvec*sin(\phivec)}) -- (P') node[pos=0.55,calibration=0.9]{\contour{white}{$z$}}; \draw[->] (\rtheta,0,0) arc(0:\thetavec:\rtheta) node[pos=0.35,beneath=-2,scale=0.9] {$\theta$}; % VECTORS \draw[vector] (O) -- (P') node[pos=0.5,above left=-iv] {$r$} node[right=1,higher up right=-3] {$\mathrm{P} = (\rho;\theta;z)$}; \end{tikzpicture} % 3D AXIS with cylindrical coordinates with dark unit vectors \tdplotsetmaincoords{lx}{110} \begin{tikzpicture}[calibration=two.2,tdplot_main_coords] % VARIABLES \def\50{0.thirty} % length scale nighttime unit vector \def\rtheta{0.vii*\fifty} % length theta arc \def\rvec{ane.ii} \def\phivec{46} \def\thetavec{48} % AXES \coordinate (O) at (0,0,0); \tdplotsetcoord{P}{\rvec}{\phivec}{\thetavec} \draw[dashed,myblue] (O) -- (Pxy); \describe[thick,->] (0,0,0) -- (1,0,0) node[beneath left=-iii]{$ten$}; \describe[thick,->] (0,0,0) -- (0,1,0) node[right=-1]{$y$}; \draw[thick,->] (0,0,0) -- (0,0,ane) node[above=-ane]{$z$}; \draw (Pxy)++(0,0,0.12) --++ (\thetavec+180:0.12) --++ (0,0,-0.12); % VECTORS & DASHED \depict[dashed,mydarkblue] (P) -- (Pz) node[pos=0.55,higher up correct=-6] {\profile{white}{$\rho$}}; \draw[dashed,mydarkblue] (Py) -- (Pxy) -- (Px); % MEASURES \depict[->,veccol] (0,0,0) -- (\thetavec:{\rvec*sin(\phivec)}) node[myblue,pos=0.65,scale=0.ix]{\contour{white}{$\rho$}}; \draw[<->,veccol] (\thetavec:{\rvec*sin(\phivec)}) -- (P') node[myblue,pos=0.55,scale=0.9]{\contour{white}{$z$}}; \draw[->] (\rtheta,0,0) arc(0:\thetavec:\rtheta) node[pos=0.35,below=-2,calibration=0.ix] {$\theta$}; % UNITT VECTORS \draw[dark unit of measurement vector] (0,0,0) -- (\thetavec:1.two*\50) node[left=iii,below=-iii,scale=0.8]{$\vu*{\rho}$}; \describe[dark unit vector] (0,0,0) -- (\thetavec+xc:\l) node[above=two.v,right=-2.5,calibration=0.eight]{$\vu*{\theta}$}; \depict[dark unit vector] (0,0,0) -- (0,0,\l) node[left,calibration=0.8]{$\vu{z}$}; % VECTORS \node[circumvolve,inner sep=0.nine,fill=myblue] (P') at ({\rvec*sin(\phivec)*cos(\thetavec)},{\rvec*sin(\phivec)*sin(\thetavec)},{\rvec*cos(\phivec)}) {}; \depict[vector] (O) -- (P') node[pos=0.5,to a higher place left=-four] {$r$} node[right=1,above right=-3] {$\mathrm{P} = (\rho;\theta;z)$}; \end{tikzpicture} % 3D Centrality with polar coordinates \tdplotsetmaincoords{60}{110} \brainstorm{tikzpicture}[scale=two.2,tdplot_main_coords] % VARIABLES \def\l{0.thirty} % length scale night unit vector \def\rtheta{0.7*\l} % length theta arc \def\rvec{1.2} \def\phivec{46} \def\thetavec{48} % AXES \coordinate (O) at (0,0,0); \tdplotsetcoord{P}{\rvec}{\phivec}{\thetavec} \depict[dashed,myblue] (O) -- (Pxy); \depict[thick,->] (0,0,0) -- (1,0,0) node[below left=-three]{$x$}; \draw[thick,->] (0,0,0) -- (0,i,0) node[right=-1]{$y$}; \draw[thick,->] (0,0,0) -- (0,0,one) node[above=-one]{$z$}; \draw (Pxy)++(0,0,0.12) --++ (\thetavec+180:0.12) --++ (0,0,-0.12); % VECTORS & DASHED %\draw[dashed,mydarkblue] (P) -- (Pxy); \draw[dashed,mydarkblue] (P) -- (Pz) node[pos=0.55,above right=-v] {\profile{white}{$r$}}; \draw[dashed,mydarkblue] (Py) -- (Pxy) -- (Px); % MEASURES %\draw[->,veccol] (0,0,0) -- (\thetavec:{\rvec*sin(\phivec)}) node[pos=0.75,above=0,scale=0.9]{$r$}; \draw[->,veccol] (0,0,0) -- (\thetavec:{\rvec*sin(\phivec)}) node[myblue,pos=0.65,scale=0.9]{\contour{white}{$r$}}; %\draw[<->,veccol] (\thetavec:{\rvec*sin(\phivec)}) --++ (0,0,{\rvec*cos(\phivec)}) \describe[<->,veccol] (\thetavec:{\rvec*sin(\phivec)}) -- (P') node[myblue,pos=0.55,calibration=0.9]{\profile{white}{$z$}}; \depict[->] (\rtheta,0,0) arc(0:\thetavec:\rtheta) node[pos=0.35,below=-2,scale=0.9] {$\theta$}; % UNITT VECTORS \draw[dark unit vector] (0,0,0) -- (\thetavec:1.2*\50) node[left=2,below=-3,scale=0.viii]{$\vu{r}$}; \describe[dark unit vector] (0,0,0) -- (\thetavec+90:\50) node[above=2.5,right=-2.5,scale=0.8]{$\vu*{\theta}$}; \draw[dark unit vector] (0,0,0) -- (0,0,\l) node[left,scale=0.8]{$\vu{z}$}; % VECTORS \node[circle,inner sep=0.nine,fill up=myblue] (P') at ({\rvec*sin(\phivec)*cos(\thetavec)},{\rvec*sin(\phivec)*sin(\thetavec)},{\rvec*cos(\phivec)}) {}; \describe[vector] (O) -- (P') node[right=i,in a higher place right=-iii] {$\mathrm{P} = (r;\theta;z)$}; \cease{tikzpicture} % 3D AXIS with spherical coordinates, dA \tdplotsetmaincoords{60}{103} \brainstorm{tikzpicture}[scale=2.viii,tdplot_main_coords] % VARIABLE \def\rvec{one.0} \def\thetavec{35} \def\phivec{45} \def\dtheta{10} \def\dphi{16} \def\sphere#1#2#iii{plot[domain=#1]({\rvec*sin(#2)*cos(#3)},{\rvec*sin(#two)*sin(#iii)},{\rvec*cos(#ii)})} \contourlength{0.8pt} % AXES \coordinate (O) at (0,0,0); \draw[thick,->] (0,0,0) -- (1.16*\rvec,0,0) node[left=2,beneath]{$x$}; \draw[thick,->] (0,0,0) -- (0,1.one*\rvec,0) node[below=ii,correct=0]{$y$}; \draw[thick,->] (0,0,0) -- (0,0,1.1*\rvec) node[above]{$z$}; % COORDINATES \tdplotsetcoord{P}{\rvec}{\thetavec}{\phivec} \tdplotsetcoord{Lead}{\rvec}{\thetavec+\dtheta}{\phivec} \tdplotsetcoord{PR}{\rvec}{\thetavec}{\phivec+\dphi} \tdplotsetcoord{PBR}{\rvec}{\thetavec+\dtheta}{\phivec+\dphi} % CONE \depict[veccol!twenty,very thin] (O) -- (PBR); \draw[veccol!twenty,very sparse] (O) -- (PR); \draw[->,veccol] (O) -- (P) node[below=five,left=2] {$\vb{r}$}; \draw[veccol,very thin] (O) -- (Atomic number 82); % PROJECTIONS \describe[proj] %\thetavec+\dtheta plot[domain=0:90]({\rvec*sin(\x)*cos(\phivec)},{\rvec*sin(\ten)*sin(\phivec)},{\rvec*cos(\10)}) coordinate (BL); \draw[proj] plot[domain=0:ninety]({\rvec*sin(\ten)*cos(\phivec+\dphi)},{\rvec*sin(\10)*sin(\phivec+\dphi)},{\rvec*cos(\x)}) coordinate (BR); \draw[proj] plot[domain=0:90]({\rvec*cos(\x)},{\rvec*sin(\x)},0); \describe[proj] (O) -- (BL); % PBxy \draw[proj] (O) -- (BR); % PBRxy \draw[proj] (P) -- (Pz); \describe[proj] (PR) -- (Pz) node[midway,above=-two,rotate=-24] {\contour{white}{$r\sin\theta$}}; %\draw[proj,projcol!xv,dashed] (P) -- (Pxy); %\draw[proj,projcol!15,dashed] (PR) -- (PRxy); %\depict[proj,projcol!15,dashed] (Lead) -- (PBxy); %\draw[proj,projcol!15,dashed] (PBR) -- (PBRxy); % Expanse \draw[area] plot[domain=0:.99*\dphi]({\rvec*sin(\thetavec)*cos(\phivec+\10)},{\rvec*sin(\thetavec)*sin(\phivec+\x)},{\rvec*cos(\thetavec)}) -- plot[domain=0:.99*\dtheta]({\rvec*sin(\thetavec+\x)*cos(\phivec+\dphi)},{\rvec*sin(\thetavec+\x)*sin(\phivec+\dphi)},{\rvec*cos(\thetavec+\x)}) -- plot[domain=.99*\dphi:0]({\rvec*sin(\thetavec+\dtheta)*cos(\phivec+\x)},{\rvec*sin(\thetavec+\dtheta)*sin(\phivec+\x)},{\rvec*cos(\thetavec+\dtheta)}) -- plot[domain=.99*\dtheta:0]({\rvec*sin(\thetavec+\x)*cos(\phivec)},{\rvec*sin(\thetavec+\ten)*sin(\phivec)},{\rvec*cos(\thetavec+\x)}) -- bike; % MEASURES %\node[right=3,beneath right=-2] at (Atomic number 82) {$r\sin\theta\dd{\phi}$}; %\node[right=5,beneath right=-2] at (PR) {$r\dd{\theta}$}; \draw[<->,proj,sparse] plot[domain=0:\dphi]({\rvec*sin(\thetavec+1.11*\dtheta)*cos(\phivec+\ten)},{\rvec*sin(\thetavec+ane.11*\dtheta)*sin(\phivec+\10)},{\rvec*cos(\thetavec+1.xi*\dtheta)}) node[correct=12,below] {\contour{white}{$r\sin\theta\dd{\phi}$}}; \draw[<->,proj,sparse] plot[domain=0:\dtheta]({\rvec*sin(\thetavec+\ten)*cos(\phivec+1.15*\dphi)},{\rvec*sin(\thetavec+\10)*sin(\phivec+1.15*\dphi)},{\rvec*cos(\thetavec+\x)}) node[in a higher place=11,right=-3] {$r\dd{\theta}$}; % ANGLES \tdplotdrawarc[->]{(O)}{0.35*\rvec}{0}{\phivec} {below=-2}{$\phi$} \tdplotdrawarc[->]{(O)}{0.45*\rvec}{\phivec}{\phivec+\dphi} {anchor=145,inner sep=one}{\profile{white}{$\dd{\phi}$}} \tdplotsetthetaplanecoords{\phivec} \tdplotdrawarc[->,tdplot_rotated_coords]{(0,0,0)}{0.36*\rvec}{0}{\thetavec} {right=2,above=-one}{$\theta$} \tdplotdrawarc[->,tdplot_rotated_coords]{(0,0,0)}{0.54*\rvec}{\thetavec}{\thetavec+\dtheta} {left=0.2,to a higher place correct=-2}{\profile{white}{$\dd{\theta}$}} \cease{tikzpicture} % SOLID Angle SURFACE INTEGRATION \begin{tikzpicture} % VARIABLE \def\R{three.eight} \def\ang{5} \def\angII{forty} \coordinate (O) at (0,0); \coordinate (P) at (\ang:\R); \coordinate (Pr) at (\ang:\R-0.25); % SURFACE \fill[top color=white,bottom colour=blue!20,eye colour=white,shading angle=\angII+95] (\ang+20:0.8*\R) to[out=-15,in=130] (\ang:1.1*\R) to[out=-50,in=80] (\ang-xv:1.2*\R) to[out=150,in=-70] cycle; \depict[blue!80!blackness!eighty] (\ang+20:0.8*\R) to[out=-15,in=130] (\ang:1.1*\R) to[out=-50,in=80] (\ang-15:1.ii*\R); % CONE \draw[unit vector] (0,0) -- (P); % node[left=3,below left=2] {$\vb{r}$}; %\begin{scope} % \prune[shift={(P)},rotate around={22:(P)}] % (-0.four,0) rectangle ++(0.8,0.8) -- bicycle; % \describe[depict=bluish!80,fill=blue!80,make full opacity=0.half dozen,rotate around={\angII:(P)},fill opacity=0.4] % (P) ellipse (0.2 and 0.iv); %\finish{scope} \depict[area,fill opacity=0.4,rotate effectually={\ang:(Pr)}] (Pr)++(ninety+\ang:0.006*\R) ellipse (0.2 and 0.375); \draw[draw=bluish!80,fill=blueish!lxxx,fill opacity=0.iv,rotate around={\angII:(P)}] (P) ellipse (0.2 and 0.468); %\begin{scope} % \prune[shift={(P)},rotate effectually={22:(P)}] % (-0.4,0) rectangle ++(0.8,-0.8) -- cycle; % \draw[draw=blue!80,fill=blue!lxxx,fill opacity=0.vi,rotate around={\angII:(P)},fill opacity=0.four] % (P) ellipse (0.2 and 0.4); %\finish{scope} \draw[dashed,proj] (P)++(\angII+84:0.464) coordinate (PT) -- (0,0); \draw[dashed,proj] (P)++(\angII-96:0.468) coordinate (PB) node[blue!ninety,correct=iii,below=-1,scale=0.eight] {$\dd{A}$} -- (0,0); \node[veccol,left=11,below=10,calibration=0.8] at (Pr) {$\cos\theta\dd{A}$}; % VECTORS \draw[unit of measurement vector,blue!lxxx] (P) --++ (\angII:0.28*\R) coordinate (N) node[above=ane,right] {$\vu{n}$}; \describe[dark unit vector] (P) --++ (\ang:0.28*\R) coordinate (R) node[correct] {$\vu{r}$}; \draw motion picture[->,"$\theta$",describe=blackness,angle radius=sixteen,angle eccentricity=i.4] {angle = R--P--North}; %\depict picture show[->,"$\Delta\Omega$",draw=black,angle radius=26,angle eccentricity=1.4] {angle = Atomic number 82--O--PT}; \cease{tikzpicture} \cease{document} Click to download: axis3D.tex • axis3D.pdf
Open in Overleaf: axis3D.tex
Source: https://tikz.net/axis3d/
0 Response to "how to draw 3d coordinate system"
Post a Comment